Bayesian Psychometric Model Fit Methods
Today’s Lecture Objectives
- Show how to use PPMC to evaluate absolute model fit in Bayesian psychometric models
- Show how to use LOO and WAIC for relative model fit in Bayesian psychometric models
Example Data: Conspiracy Theories
Today’s example is from a bootstrap resample of 177 undergraduate students at a large state university in the Midwest. The survey was a measure of 10 questions about their beliefs in various conspiracy theories that were being passed around the internet in the early 2010s. Additionally, gender was included in the survey. All items responses were on a 5- point Likert scale with:
- Strongly Disagree
- Disagree
- Neither Agree or Disagree
- Agree
- Strongly Agree
Please note, the purpose of this survey was to study individual beliefs regarding conspiracies. The questions can provoke some strong emotions given the world we live in currently. All questions were approved by university IRB prior to their use.
Our purpose in using this instrument is to provide a context that we all may find relevant as many of these conspiracy theories are still prevalent today.
Conspiracy Theory Questions 1-5
Questions:
- The U.S. invasion of Iraq was not part of a campaign to fight terrorism, but was driven by oil companies and Jews in the U.S. and Israel.
- Certain U.S. government officials planned the attacks of September 11, 2001 because they wanted the United States to go to war in the Middle East.
- President Barack Obama was not really born in the United States and does not have an authentic Hawaiian birth certificate.
- The current financial crisis was secretly orchestrated by a small group of Wall Street bankers to extend the power of the Federal Reserve and further their control of the world’s economy.
- Vapor trails left by aircraft are actually chemical agents deliberately sprayed in a clandestine program directed by government officials.
Conspiracy Theory Questions 6-10
Questions:
- Billionaire George Soros is behind a hidden plot to destabilize the American government, take control of the media, and put the world under his control.
- The U.S. government is mandating the switch to compact fluorescent light bulbs because such lights make people more obedient and easier to control.
- Government officials are covertly Building a 12-lane "NAFTA superhighway" that runs from Mexico to Canada through America’s heartland.
- Government officials purposely developed and spread drugs like crack-cocaine and diseases like AIDS in order to destroy the African American community.
- God sent Hurricane Katrina to punish America for its sins.
Model Setup Today
Today, we will revert back to the graded response model assumptions to discuss how to estimate the latent variable standard deviation
\[P\left(Y_{ic } = c \mid \theta_p \right) = \left\{ \begin{array}{lr} 1-P\left(Y_{i1} \gt 1 \mid \theta_p \right) & \text{if } c=1 \\ P\left(Y_{i{c-1}} \gt c-1 \mid \theta_p \right) - P\left(Y_{i{c}} \gt c \mid \theta_p \right) & \text{if } 1<c<C_i \\ P\left(Y_{i{C_i -1} } \gt C_i-1 \mid \theta_p \right) & \text{if } c=C_i \\ \end{array} \right.\]
Where:
\[ P\left(Y_{i{c}} > c \mid \theta \right) = \frac{\exp(-\tau_{ic}+\lambda_i\theta_p)}{1+\exp(-\tau_{ic}+\lambda_i\theta_p)}\]
With:
- \(C_i-1\) Ordered thresholds: \(\tau_1 < \tau_2 < \ldots < \tau_{C_i-1}\)
We can convert thresholds to intercepts by multiplying by negative one: \(\mu_c = -\tau_c\)
Model Comparisons: One vs. Two Dimensions
We will fit two models to the data:
- A unidimensional model (see Lecture 4d here)
- A two-dimensionsal model (see Lecture 4e here)
We know from previous lectures that the two-dimensional model had a correlation very close to one
- Such a high correlation made it seem implausible there were two dimensions
Posterior Predictive Model Checking for Absolute Fit in Bayesian Psychometric Models
Psychometric Model PPMC
Psychometric models can use posterior predictive model checking (PPMC) to assess how well they fit the data in an absolute sense
- Each iteration of the chain, each item is simulated using model parameter values from that iteration
- Summary statistics are used to evaluate model fit
- Univariate measures (each item, separately):
- Item mean
- Item \(\chi^2\) (comparing observed data with each simulated data set)
- Not very useful unless:
- Parameters have “obscenely” informative priors
- There are cross-item constraints on some parameters (such as all loadings are equal)
- Bivariate measures (each pair of items)
- For binary data: Tetrachoric correlations
- For polytomous data: Polychoric correlations (but difficult to estimate with small samples), pearson correlations
- For other types of data: Pearson correlations
- Univariate measures (each item, separately):
Problems with PPMC
Problems with PPMC include
- No uniform standard for which statistics to use
- Tetrachoric correlations? Pearson correlations?
- No uniform standard by which data should fit, absolutely
- Jihong Zhang has some work on this topic, though:
- Paper in Structural Equation Modeling
- Dissertation on PPMC with M2 statistics (working on publishing)
- Jihong Zhang has some work on this topic, though:
- No way to determine if a model is overparameterized (too complicated)
- Fit only improves to a limit
Implementing PPMC in Stan (one \(\theta\))
Notes:
- Generated quantities block is where to implement PPMC
- Each type of distribution also has a random number generator
- Here,
ordered_logistic_rnggoes withordered_logistic
- Here,
- Each may have some issue in types of inputs (had to go person-by-person in this block)
- Rather than have Stan calculate statistics, I will do so in R
Implementing PPMC in Stan (two \(\theta\)s)
Notes:
- Very similar to one dimension–just using the syntax from the model block within the
ordered_logistic_rngfunction
PPMC Processing
Stan generated a lot of data–but now we must take it from the format of Stan and process it:
# setting up PPMC
simData = modelOrderedLogit_samples$draws(variables = "simY", format = "draws_matrix")
colnames(simData)
dim(simData)
# set up object for storing each iteration's PPMC data
nPairs = choose(10, 2)
pairNames = NULL
for (col in 1:(nItems-1)){
for (row in (col+1):nItems){
pairNames = c(pairNames, paste0("item", row, "_item", col))
}
}PPMC Calculating in R
PPMCsamples = list()
PPMCsamples$correlation = NULL
PPMCsamples$mean = NULL
# loop over each posterior sample's simulated data
for (sample in 1:nrow(simData)){
# create data frame that has observations (rows) by items (columns)
sampleData = data.frame(matrix(data = NA, nrow = nObs, ncol = nItems))
for (item in 1:nItems){
itemColumns = colnames(simData)[grep(pattern = paste0("simY\\[", item, "\\,"), x = colnames(simData))]
sampleData[,item] = t(simData[sample, itemColumns])
}
# with data frame created, apply functions of the data:
# calculate item means
PPMCsamples$mean = rbind(PPMCsamples$mean, apply(X = sampleData, MARGIN = 2, FUN = mean))
# calculate pearson correlations
temp=cor(sampleData)
PPMCsamples$correlation = rbind(PPMCsamples$correlation, temp[lower.tri(temp)])
}PPMC Results Tabulation in R (Mean)
# next, build distributions for each type of statistic
meanSummary = NULL
# for means
for (item in 1:nItems){
tempDist = ecdf(PPMCsamples$mean[,item])
ppmcMean = mean(PPMCsamples$mean[,item])
observedMean = mean(conspiracyItems[,item])
meanSummary = rbind(
meanSummary,
data.frame(
item = paste0("Item", item),
ppmcMean = ppmcMean,
observedMean = observedMean,
residual = observedMean - ppmcMean,
observedMeanPCT = tempDist(observedMean)
)
)
}PPMC Results Tabulation in R (Correlation)
# for pearson correlations
corrSummary = NULL
# for means
for (column in 1:ncol(PPMCsamples$correlation)){
# get item numbers from items
items = unlist(strsplit(x = colnames(PPMCsamples$correlation)[column], split = "_"))
item1num = as.numeric(substr(x = items[1], start = 5, stop = nchar(items[1])))
item2num = as.numeric(substr(x = items[2], start = 5, stop = nchar(items[2])))
tempDist = ecdf(PPMCsamples$correlation[,column])
ppmcCorr = mean(PPMCsamples$correlation[,column])
observedCorr = cor(conspiracyItems[,c(item1num, item2num)])[1,2]
pct = tempDist(observedCorr)
if (pct > .975 | pct < .025){
inTail = TRUE
} else {
inTail = FALSE
}
corrSummary = rbind(
corrSummary,
data.frame(
item1 = paste0("Item", item1num),
item2 = paste0("Item", item2num),
ppmcCorr = ppmcCorr,
observedCorr = observedCorr,
residual = observedCorr - ppmcCorr,
observedCorrPCT = pct,
inTail = inTail
)
)
}
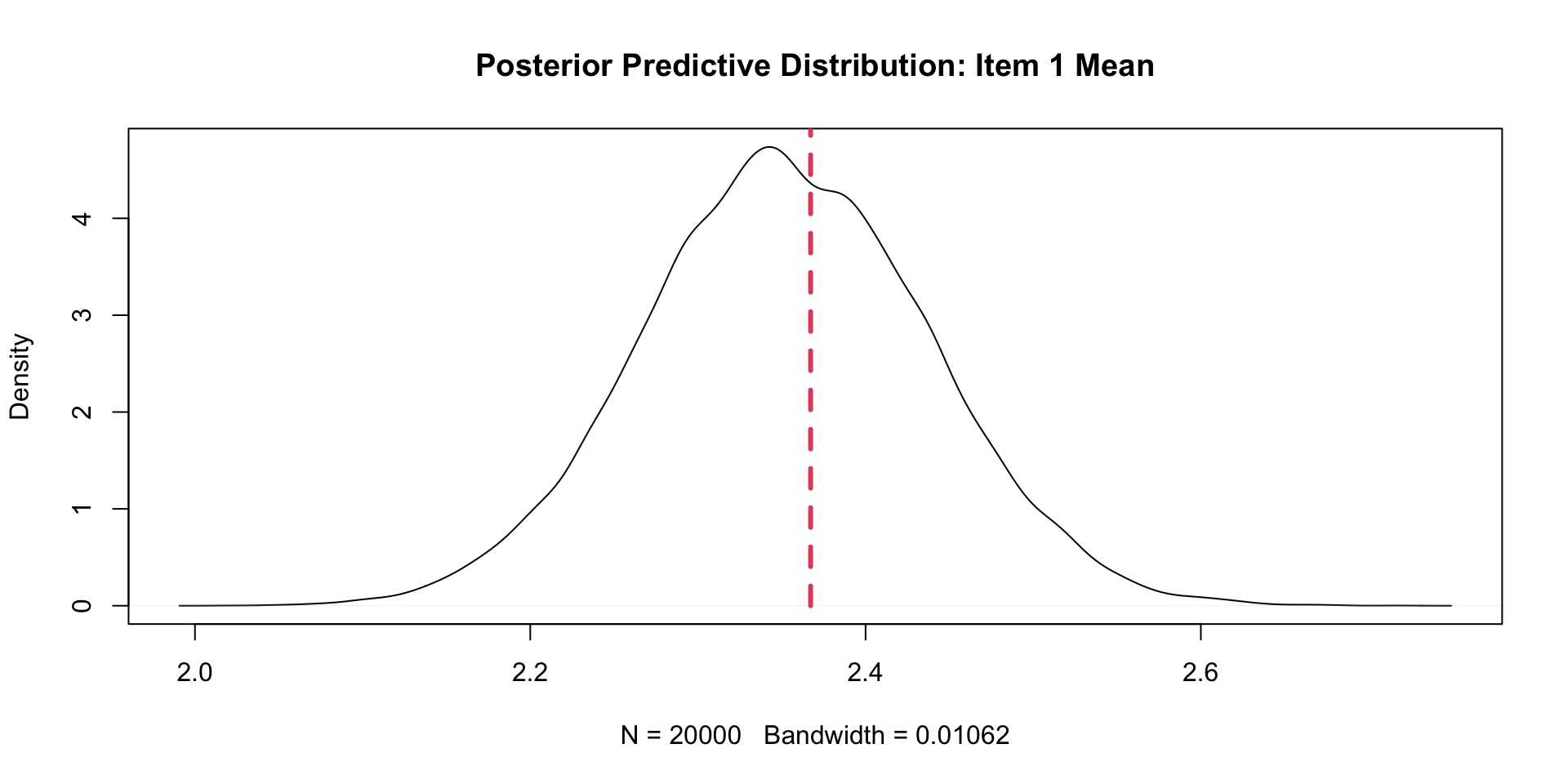
View(corrSummary)PPMC Mean Results: Example Item (One \(\theta\))
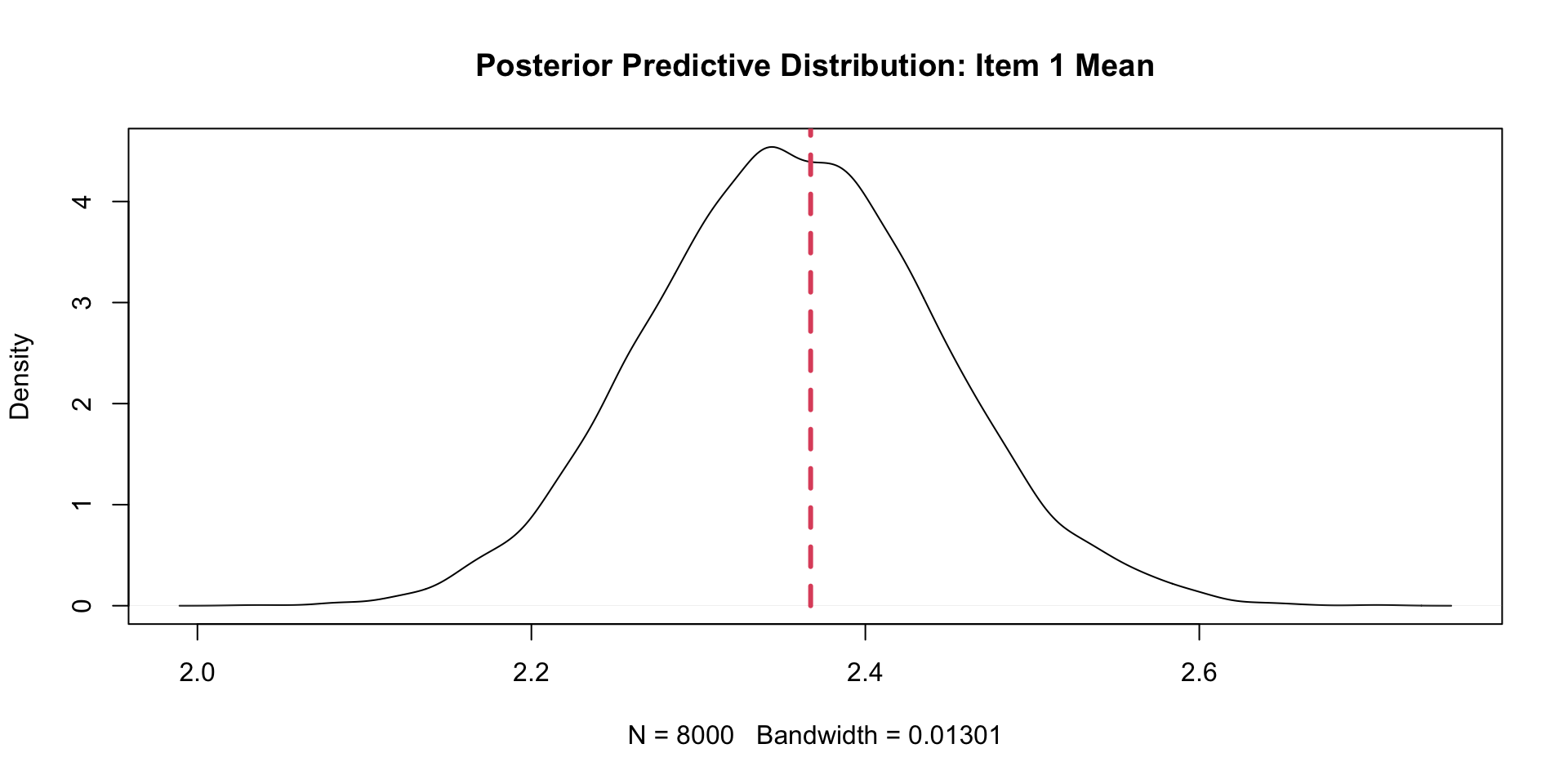
PPMC Mean Results: Example Item (Two \(\theta\)s)
PPMC Mean Results
One \(\theta\)
item ppmcMean observedMean residual observedMeanPCT
1 Item1 2.352560 2.367232 0.014671186 0.58340
2 Item2 1.958342 1.954802 -0.003539831 0.47495
3 Item3 1.862719 1.875706 0.012987571 0.58610
4 Item4 2.008068 2.011299 0.003231638 0.53915
5 Item5 1.978207 1.983051 0.004843503 0.53005
6 Item6 1.880974 1.892655 0.011681356 0.61725
7 Item7 1.748335 1.723164 -0.025171469 0.37290
8 Item8 1.840580 1.841808 0.001228249 0.51550
9 Item9 1.825317 1.807910 -0.017407062 0.43230
10 Item10 1.535198 1.519774 -0.015424294 0.45225Two \(\theta\)s
item ppmcMean observedMean residual observedMeanPCT
1 Item1 2.357626 2.367232 0.0096059322 0.559500
2 Item2 1.969614 1.954802 -0.0148114407 0.418500
3 Item3 1.874785 1.875706 0.0009216102 0.528000
4 Item4 2.016655 2.011299 -0.0053552260 0.493000
5 Item5 1.988220 1.983051 -0.0051687853 0.465375
6 Item6 1.895842 1.892655 -0.0031864407 0.500375
7 Item7 1.758951 1.723164 -0.0357874294 0.326125
8 Item8 1.853244 1.841808 -0.0114357345 0.424500
9 Item9 1.835992 1.807910 -0.0280819209 0.373625
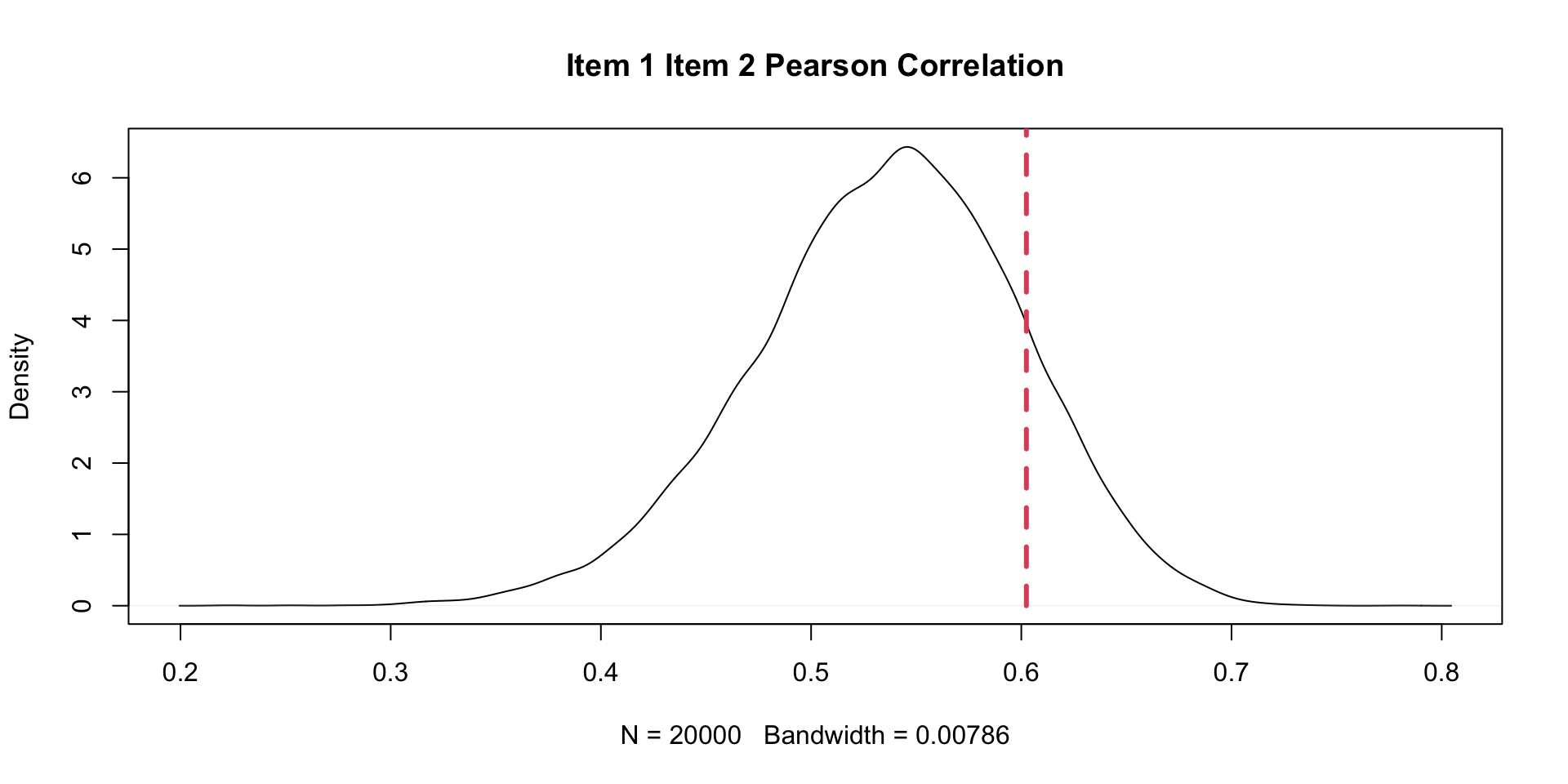
10 Item10 1.553063 1.519774 -0.0332888418 0.376125PPMC Correlation Results: Example Item Pair (One \(\theta\))
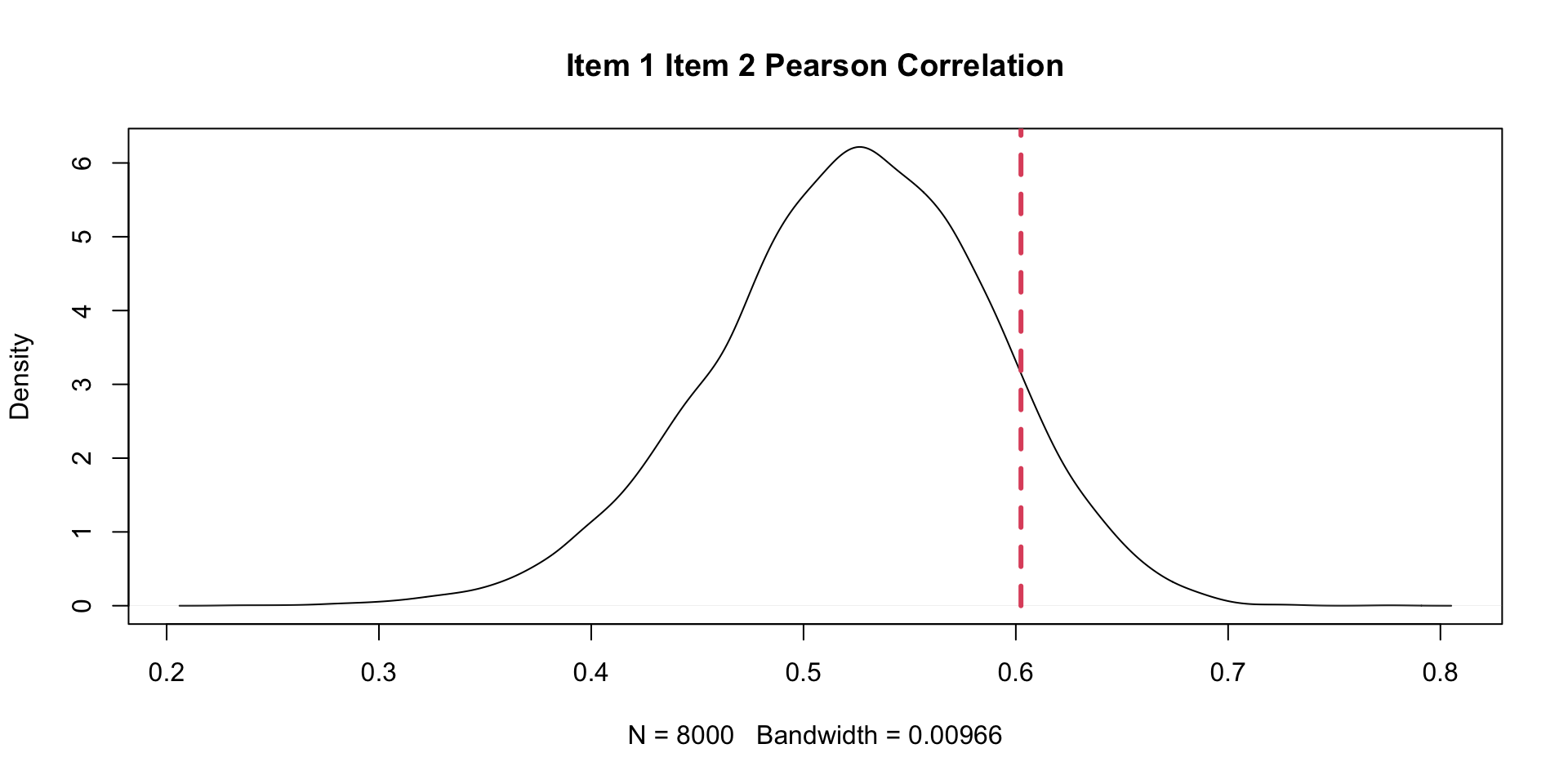
PPMC Correlation Results: Example Item Pair (Two \(\theta\)s)
PPMC Correlation Results
item1 item2 observedCorr ppmcCorr.x residual.x observedCorrPCT.x inTail.x
1 Item10 Item1 0.2568334 0.4131131 -0.156279686 0.01655 TRUE
2 Item10 Item2 0.4121264 0.4917030 -0.079576626 0.14375 FALSE
3 Item10 Item3 0.5670156 0.4522000 0.114815615 0.93835 FALSE
4 Item10 Item4 0.4516124 0.4890239 -0.037411565 0.28790 FALSE
5 Item10 Item5 0.5822203 0.5567640 0.025456304 0.62005 FALSE
6 Item10 Item6 0.5092003 0.5501939 -0.040993565 0.25890 FALSE
7 Item10 Item7 0.4420205 0.4992130 -0.057192487 0.22315 FALSE
8 Item10 Item8 0.5457127 0.5434373 0.002275470 0.48760 FALSE
9 Item10 Item9 0.4244916 0.4940797 -0.069588089 0.18525 FALSE
10 Item2 Item1 0.6024186 0.5357365 0.066682114 0.85585 FALSE
11 Item3 Item1 0.3473072 0.4931202 -0.145812943 0.01745 TRUE
12 Item3 Item2 0.5176819 0.5569093 -0.039227387 0.26420 FALSE
13 Item4 Item1 0.5700901 0.5439901 0.026099947 0.64290 FALSE
14 Item4 Item2 0.5815808 0.6090530 -0.027472228 0.30375 FALSE
15 Item4 Item3 0.4973987 0.5615192 -0.064120482 0.15380 FALSE
16 Item5 Item1 0.5526073 0.6008370 -0.048229709 0.19820 FALSE
17 Item5 Item2 0.6512768 0.6835423 -0.032265485 0.25645 FALSE
18 Item5 Item3 0.5942163 0.6288536 -0.034637387 0.26495 FALSE
19 Item5 Item4 0.6267160 0.6877014 -0.060985378 0.11495 FALSE
20 Item6 Item1 0.5435771 0.5996223 -0.056045208 0.16460 FALSE
21 Item6 Item2 0.6835282 0.6802492 0.003279028 0.49990 FALSE
22 Item6 Item3 0.6601292 0.6276426 0.032486611 0.68855 FALSE
23 Item6 Item4 0.6251455 0.6853371 -0.060191526 0.11720 FALSE
24 Item6 Item5 0.7366890 0.7696183 -0.032929309 0.18445 FALSE
25 Item7 Item1 0.4084389 0.5196236 -0.111184764 0.04695 FALSE
26 Item7 Item2 0.4721628 0.5988845 -0.126721659 0.02785 FALSE
27 Item7 Item3 0.6193269 0.5520486 0.067278349 0.83690 FALSE
28 Item7 Item4 0.4676834 0.6002957 -0.132612336 0.02010 TRUE
29 Item7 Item5 0.6204485 0.6779012 -0.057452711 0.14370 FALSE
30 Item7 Item6 0.6870303 0.6740562 0.012974158 0.57020 FALSE
31 Item8 Item1 0.5425166 0.5990322 -0.056515657 0.16485 FALSE
32 Item8 Item2 0.6317705 0.6774062 -0.045635698 0.17995 FALSE
33 Item8 Item3 0.6182736 0.6266373 -0.008363667 0.42020 FALSE
34 Item8 Item4 0.6373299 0.6835823 -0.046252488 0.17135 FALSE
35 Item8 Item5 0.7641703 0.7672351 -0.003064875 0.44260 FALSE
36 Item8 Item6 0.7557355 0.7697220 -0.013986520 0.33825 FALSE
37 Item8 Item7 0.6611475 0.6720005 -0.010853042 0.39345 FALSE
38 Item9 Item1 0.4420860 0.5114050 -0.069318985 0.14180 FALSE
39 Item9 Item2 0.5998366 0.5909206 0.008915976 0.53460 FALSE
40 Item9 Item3 0.3912734 0.5436816 -0.152408206 0.01670 TRUE
41 Item9 Item4 0.6108052 0.5917868 0.019018393 0.60460 FALSE
42 Item9 Item5 0.7119365 0.6693743 0.042562230 0.76780 FALSE
43 Item9 Item6 0.5849045 0.6643001 -0.079395555 0.07880 FALSE
44 Item9 Item7 0.5653926 0.5905836 -0.025191060 0.33045 FALSE
45 Item9 Item8 0.6068774 0.6608282 -0.053950800 0.15570 FALSE
ppmcCorr.y residual.y observedCorrPCT.y inTail.y
1 0.4062453 -0.149411838 0.021375 TRUE
2 0.4741188 -0.061992441 0.208000 FALSE
3 0.4396909 0.127324771 0.954625 FALSE
4 0.4789946 -0.027382240 0.337625 FALSE
5 0.5336977 0.048522599 0.736750 FALSE
6 0.5316488 -0.022448494 0.350250 FALSE
7 0.4725387 -0.030518156 0.338000 FALSE
8 0.5166837 0.029028985 0.646500 FALSE
9 0.4749625 -0.050470922 0.258750 FALSE
10 0.5225588 0.079859795 0.897625 FALSE
11 0.4845009 -0.137193683 0.025250 FALSE
12 0.5407355 -0.023053619 0.348375 FALSE
13 0.5350439 0.035046168 0.693625 FALSE
14 0.5943265 -0.012745647 0.396500 FALSE
15 0.5518686 -0.054469852 0.197875 FALSE
16 0.5823830 -0.029775722 0.296250 FALSE
17 0.6655675 -0.014290652 0.375000 FALSE
18 0.6060217 -0.011805479 0.396875 FALSE
19 0.6653200 -0.038603963 0.219375 FALSE
20 0.5827271 -0.039150054 0.242750 FALSE
21 0.6534385 0.030089655 0.701875 FALSE
22 0.6077661 0.052363175 0.802875 FALSE
23 0.6669047 -0.041759184 0.201375 FALSE
24 0.7328579 0.003831089 0.509500 FALSE
25 0.5004824 -0.092043558 0.087625 FALSE
26 0.5787187 -0.106555900 0.051250 FALSE
27 0.5271264 0.092200572 0.912500 FALSE
28 0.5763177 -0.108634364 0.048625 FALSE
29 0.6497289 -0.029280447 0.293375 FALSE
30 0.6379156 0.049114716 0.802500 FALSE
31 0.5730756 -0.030559026 0.295375 FALSE
32 0.6518795 -0.020108970 0.331750 FALSE
33 0.5950893 0.023184359 0.626625 FALSE
34 0.6538394 -0.016509531 0.355250 FALSE
35 0.7305302 0.033640008 0.771125 FALSE
36 0.7215552 0.034180334 0.770375 FALSE
37 0.6364697 0.024677809 0.647000 FALSE
38 0.5001129 -0.058026879 0.189375 FALSE
39 0.5797217 0.020114922 0.602250 FALSE
40 0.5287277 -0.137454306 0.028625 FALSE
41 0.5774416 0.033363627 0.688875 FALSE
42 0.6522837 0.059652847 0.848125 FALSE
43 0.6383018 -0.053397216 0.170875 FALSE
44 0.5700175 -0.004624969 0.456375 FALSE
45 0.6362707 -0.029393327 0.285125 FALSECount of Items in Misfitting Pairs
One \(\theta\)
badItems
Item1 Item3 Item10 Item4 Item7 Item9
2 2 1 1 1 1 Two \(\theta\)s
badItems2
Item1 Item10
1 1 Plotting Misfitting Items (One \(\theta\))
Relative Model Fit in Bayesian Psychometric Models
Relative Model Fit in Bayesian Psychometric Models
As with other Bayesian models, we can use WAIC and LOO to compare the model fit of two Bayesian models
- Of note: There is some debate as to whether or not we should marginalize across the latent variables
- We won’t do that here as that would involve a numeric integral
- What is needed: The conditional log likelihood for each observation at each step of the chain
- Here, we have to sum the log likelihood across all items
- There are built-in functions in Stan to do this
Implementing ELPD in Stan (one \(\theta\))
generated quantities{
// for LOO/WAIC:
vector[nObs] personLike = rep_vector(0.0, nObs);
for (item in 1:nItems){
for (obs in 1:nObs){
// calculate conditional data likelihood for LOO/WAIC
personLike[obs] = personLike[obs] + ordered_logistic_lpmf(Y[item, obs] | lambda[item]*theta[obs], thr[item]);
}
}
}Notes:
ordered_logistic_lpmfneeds the observed data to work (first argument)vector[nObs] personLike = rep_vector(0.0, nObs);is needed to set the values to zero at each iteration
Implementing ELPD in Stan (two \(\theta\)s)
generated quantities{
// for LOO/WAIC:
vector[nObs] personLike = rep_vector(0.0, nObs);
for (item in 1:nItems){
for (obs in 1:nObs){
// calculate conditional data likelihood for LOO/WAIC
personLike[obs] = personLike[obs] + ordered_logistic_lpmf(Y[item, obs] | thetaMatrix[obs,]*lambdaMatrix[item,1:nFactors]', thr[item]);
}
}
}Notes:
ordered_logistic_lpmfneeds the observed data to work (first argument)vector[nObs] personLike = rep_vector(0.0, nObs);is needed to set the values to zero at each iteration
Comparing WAIC Values
Computed from 20000 by 177 log-likelihood matrix
Estimate SE
elpd_waic -1482.6 70.4
p_waic 137.7 5.1
waic 2965.2 140.8
173 (97.7%) p_waic estimates greater than 0.4. We recommend trying loo instead.
Computed from 8000 by 177 log-likelihood matrix
Estimate SE
elpd_waic -1490.6 68.0
p_waic 142.6 4.6
waic 2981.1 136.1
174 (98.3%) p_waic estimates greater than 0.4. We recommend trying loo instead. Smaller is better, so the unidimensional model wins (but very high SE for both)
Comparing LOO Values
Computed from 20000 by 177 log-likelihood matrix
Estimate SE
elpd_loo -1542.0 71.0
p_loo 197.1 5.8
looic 3084.0 141.9
------
Monte Carlo SE of elpd_loo is NA.
Pareto k diagnostic values:
Count Pct. Min. n_eff
(-Inf, 0.5] (good) 0 0.0% <NA>
(0.5, 0.7] (ok) 4 2.3% 426
(0.7, 1] (bad) 156 88.1% 31
(1, Inf) (very bad) 17 9.6% 10
See help('pareto-k-diagnostic') for details.
Computed from 8000 by 177 log-likelihood matrix
Estimate SE
elpd_loo -1541.3 68.1
p_loo 193.2 5.1
looic 3082.5 136.2
------
Monte Carlo SE of elpd_loo is NA.
Pareto k diagnostic values:
Count Pct. Min. n_eff
(-Inf, 0.5] (good) 1 0.6% 743
(0.5, 0.7] (ok) 19 10.7% 42
(0.7, 1] (bad) 135 76.3% 4
(1, Inf) (very bad) 22 12.4% 4
See help('pareto-k-diagnostic') for details.LOO seems to (slightly) prefer the two-dimensional model (but by warnings about bad PSIS)
Comparing LOO Values
loo_compare(list(unidimensional = modelOrderedLogit_samples$loo(variables = "personLike"),
twodimensional = modelOrderedLogit2D_samples$loo(variables = "personLike"))) elpd_diff se_diff
twodimensional 0.0 0.0
unidimensional -0.7 4.9 Again, both models are very close in fit
Wrapping Up
Wrapping Up
Model fit is complicated for psychometric models
- Bayesian model fit methods are even more complicated than non-Bayesian methods
- Open area for research!
Thank you for a great semester